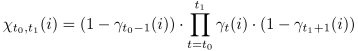
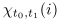 ,
the probability of staying at state
,
the probability of staying at state
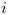 from time
from time
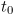 to
to
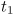 given an observation sequence
given an observation sequence
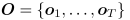 of length
of length
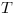 ,
as
,
as
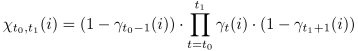
where
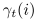 is the probability of being in state
is the probability of being in state
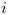 at time
at time
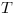 ,
and we defined
,
and we defined
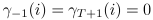 .
Based on
.
Based on
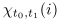 ,
the mean
,
the mean
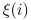 and the variance
and the variance
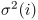 of the state duration density
of state
of the state duration density
of state
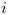 is obtained as
is obtained as
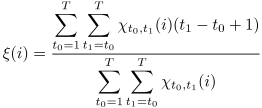
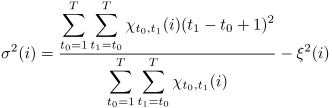
However,
the previous definition of
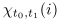 is statistially incorrect
because the state transitions were not taken into account.
is statistially incorrect
because the state transitions were not taken into account.
We redefine
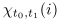 in a statistically correct manner as
in a statistically correct manner as
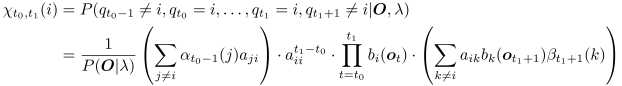
where
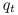 denotes the state at time
denotes the state at time
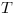 ,
,
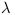 denotes the parmeter set of the HMM,
denotes the parmeter set of the HMM,
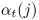 and
and
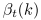 denote
the forward and backward variables,
and
denote
the forward and backward variables,
and
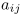 and
and
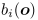 denote the state transition probability and the output probability,
respectively.
denote the state transition probability and the output probability,
respectively.